Metamaterials and Metasurfaces
Based on our previous discussion of complex refractive index (N) involving real (n) and complex parts (k), there can be multiple scenarios dictating the behavior of EM waves passing through a material. These scenarios are explained below.
1) The value of k is positive: This represents that the material is lossy and absorbing the EM wave. Natural materials are lossy if they have a non-zero value of k.
2) The value of k is negative: This scenario indicates that the material is a gain-material. These types of materials are not found in nature and have to be particularly designed.
3) The value of n is positive and n>1: Positive n represents that the EM wave slows down as it enters the material. All the naturally occurring materials slow down EM waves meaning they have a real part of the refractive index greater than 1.
4) The value of the n is positive and 0<n<1: This scenario indicates that the EM wave speeds up as it traverses this particular type of material. This conclusion is counterintuitive as nothing can travel faster than the speed of light. However, this fact exists because there is another type of speed known as phase velocity that gets higher to satisfy this increase in speed. The speed of an EM wave cannot increase beyond the speed of light but phase velocity can. For x-rays, this fact is found to be true for particular materials.
5) The value of n is negative: These types of materials are artificially made and are known as Metamaterials (other names include left-handed materials, negative refractive index-NRI materials, and double-negative materials).
Decription of Metamaterials and metasurfaces?
The term “Metamaterial” is derived from Latin where meta means beyond and material indicates naturally occurring materials. In essence metamaterials as a whole means materials having properties that are different from naturally occurring materials. The term metamaterials were first coined by Veselago. Metamaterials require both relative permittivity and relative permeability of materials to be simultaneously negative (that is why they are sometimes referred to as Double Negative Materials). This property of being double negative also satisfies the equation of calculating refractive index from permittivity and permeability.
Being a double negative material, the propagation of EM waves is also reversed in such materials.
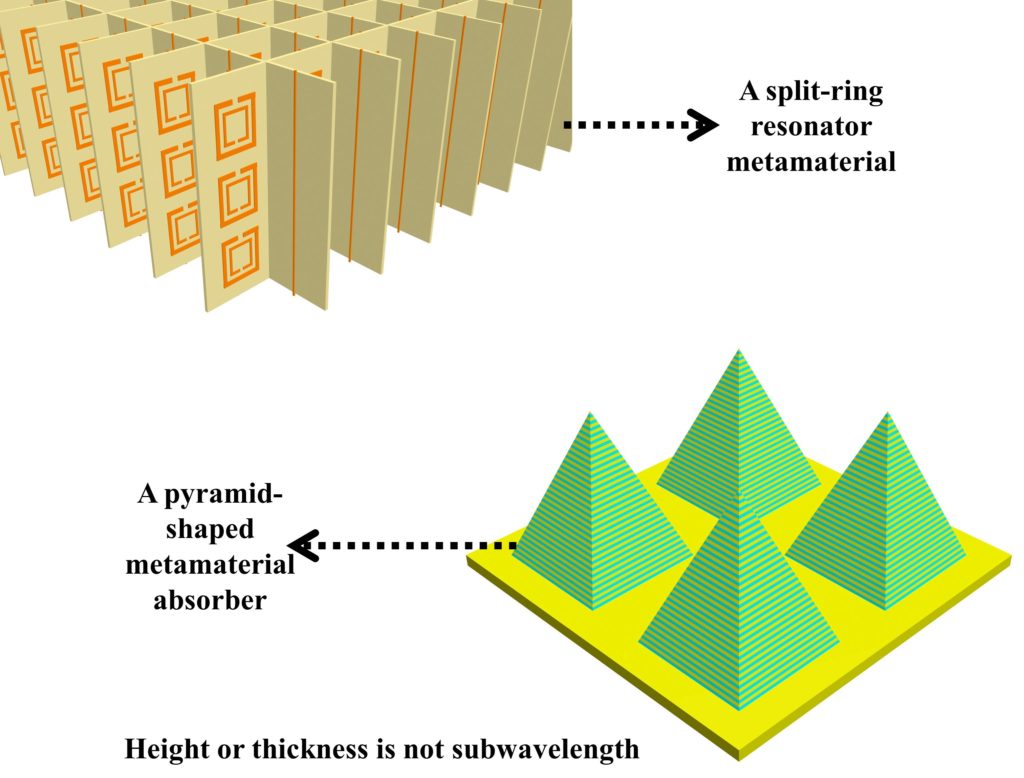
Metamaterials are subwavelength (having significantly smaller dimensions than the operating wavelength) periodic structures of natural materials that can shape the incoming EM waves by giving control over permittivity (ε). permeability (μ), and in turn over complex refractive index (N). A few typical examples of metamaterials are shown in Fig. 1.
MEtasurfaces
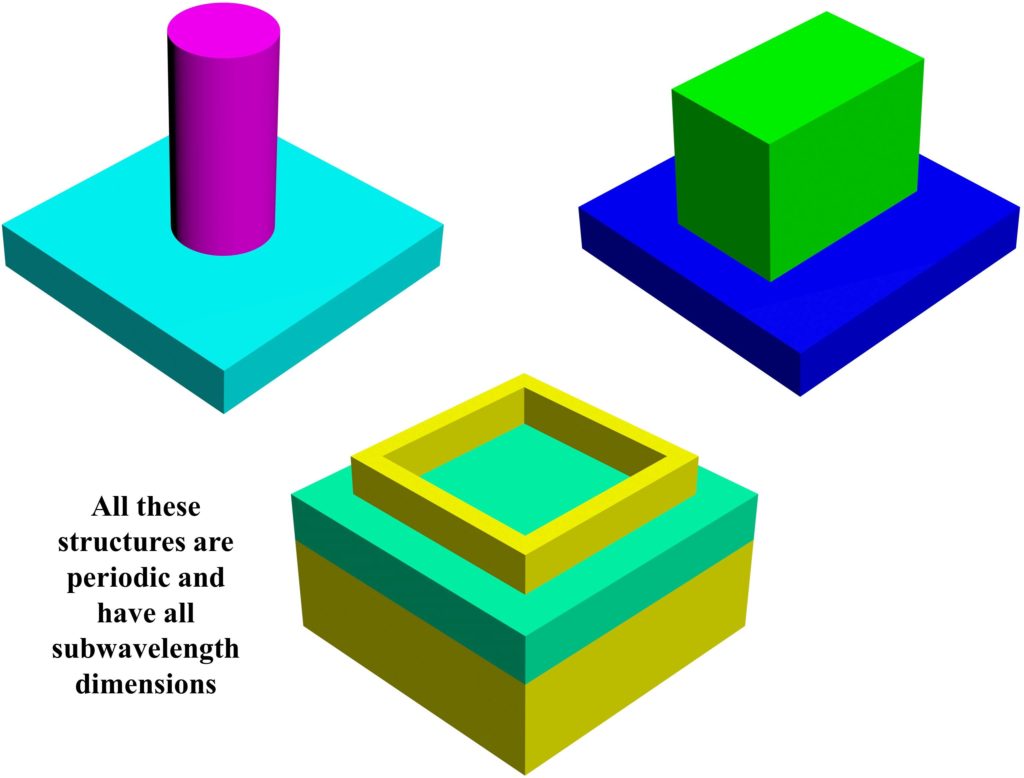
The metamaterials discussed in the previous section did not have subwavelength thickness or height. Metasurfaces are counterparts of metamaterials, however, they also have subwavelength thickness/height. Metasurfaces have lower dimensions and therefore less bulky in comparison to metamaterials, and this why, in some literature, they are referred to as single-layer metamaterials. A few examples of metasurfaces are shown in Fig. 2 below.
Advantages of metamaterials and metasurfaces
Metamaterials and metasurfaces offer significant advantages in the field of optics when compared to conventional optical elements. A few key advantages are mentioned below.
- Metamaterials and metasurfaces offer subwavelength imaging that is imaging below the diffraction limit. Optical microscopes are limited in their resolution, which is defined by the diffraction limit. An optical EM wave with a wavelength of λ, traveling through the material with real refractive index (n), with a half-angle θ, will have the least resolvable distance (d) as follows. The tern nsinθ is the numerical aperture (NA) and the least resolvable distance comes for NA of 1. Therefore, for 633 nm wavelength (red light), the minimum resolvable distance would be around 316.5 nm. However, by employing metamaterials and metasurfaces, we can get an even smaller resolvable distance.

- Metamaterials and metasurfaces are less bulky than conventional materials since they can achieve desired phase change due to their design. In comparison, the conventional optical elements such as lenses achieved the desired phase change by increasing the thickness.
- Through metamaterials and metasurfaces, control over permittivity (ε). permeability (μ) is achieved that helps to realize optical phenomena not found in nature. Some of these exotic phenomena are discussed in the next few posts. Some of these phenomena include metasurface lens or metalens, metasurface hologram or metahologram, and metasurface absorbers.
